Zero–sum game
From Wikipedia, the free encyclopedia
|
|
This article needs attention from an expert on the subject. Please add a reason or a talk parameter to this template to explain the issue with the article. WikiProject Game theory may be able to help recruit an expert. (March 2011) |
In
game theory and
economic theory, a
zero-sum game is a
mathematical representation of a situation in which a participant's gain (or loss) of
utility
is exactly balanced by the losses (or gains) of the utility of the
other participant(s). If the total gains of the participants are added
up, and the total losses are subtracted, they will sum to zero. Thus
cutting a cake,
where taking a larger piece reduces the amount of cake available for
others, is a zero-sum game if all participants value each unit of cake
equally (see
marginal utility). In contrast,
non-zero-sum
describes a situation in which the interacting parties' aggregate gains
and losses are either less than or more than zero. A zero-sum game is
also called a
strictly competitive game while non-zero-sum games can be either competitive or non-competitive. Zero-sum games are most often solved with the
minimax theorem which is closely related to
linear programming duality,
[1] or with
Nash equilibrium.
Definition
The zero-sum property (if one gains, another loses) means that any result of a zero-sum situation is
Pareto optimal (generally, any game where all strategies are Pareto optimal is called a conflict game).
[2]
Situations where participants can all gain or suffer together are
referred to as non-zero-sum. Thus, a country with an excess of bananas
trading with another country for their excess of apples, where both
benefit from the transaction, is in a non-zero-sum situation. Other
non-zero-sum games are games in which the sum of gains and losses by the
players are sometimes more or less than what they began with.
Solution
For 2-player finite zero-sum games, the different
game theoretic solution concepts of
Nash equilibrium,
minimax, and
maximin all give the same solution. In the solution, players play a
mixed strategy.
Example
A zero-sum game
|
A |
B |
C |
| 1 |
30, -30 |
-10, 10 |
20, -20 |
| 2 |
10, -10 |
20, -20 |
-20, 20 |
A game's
payoff matrix is a convenient representation. Consider for example the two-player zero-sum game pictured at right.
The order of play proceeds as follows: The first player (red) chooses
in secret one of the two actions 1 or 2; the second player (blue),
unaware of the first player's choice, chooses in secret one of the three
actions A, B or C. Then, the choices are revealed and each player's
points total is affected according to the payoff for those choices.
Example: Red chooses action 2 and Blue chooses action B. When the
payoff is allocated, Red gains 20 points and Blue loses 20 points.
Now, in this example game both players know the payoff matrix and
attempt to maximize the number of their points. What should they do?
Red could reason as follows: "With action 2, I could lose up to 20
points and can win only 20, while with action 1 I can lose only 10 but
can win up to 30, so action 1 looks a lot better." With similar
reasoning, Blue would choose action C. If both players take these
actions, Red will win 20 points. But what happens if Blue anticipates
Red's reasoning and choice of action 1, and goes for action B, so as to
win 10 points? Or if Red in turn anticipates this devious trick and goes
for action 2, so as to win 20 points after all?
Émile Borel and
John von Neumann had the fundamental and surprising insight that
probability
provides a way out of this conundrum. Instead of deciding on a definite
action to take, the two players assign probabilities to their
respective actions, and then use a random device which, according to
these probabilities, chooses an action for them. Each player computes
the probabilities so as to minimize the maximum
expected point-loss independent of the opponent's strategy. This leads to a
linear programming problem with the optimal strategies for each player. This
minimax method can compute provably optimal strategies for all two-player zero-sum games.
For the example given above, it turns out that Red should choose
action 1 with probability 4/7 and action 2 with probability 3/7, while
Blue should assign the probabilities 0, 4/7, and 3/7 to the three
actions A, B, and C. Red will then win 20/7 points on average per game.
Solving
The
Nash equilibrium for a two-player, zero-sum game can be found by solving a
linear programming problem. Suppose a zero-sum game has a payoff matrix
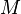
where element

is the payoff obtained when the minimizing player chooses pure strategy
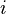
and the maximizing player chooses pure strategy
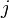
(i.e. the player trying to minimize the payoff chooses the row and the
player trying to maximize the payoff chooses the column). Assume every
element of
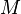
is positive. The game will have at least one Nash equilibrium. The Nash
equilibrium can be found (see ref. [2], page 740) by solving the
following linear program to find a vector

:
- Minimize:
-

- Subject to the constraints:
 ≥ 0
≥ 0 ≥ 1.
≥ 1.
The first constraint says each element of the

vector must be nonnegative, and the second constraint says each element of the

vector must be at least 1. For the resulting

vector, the inverse of the sum of its elements is the value of the game. Multiplying

by that value gives a probability vector, giving the probability that
the maximizing player will choose each of the possible pure strategies.
If the game matrix does not have all positive elements, simply add a
constant to every element that is large enough to make them all
positive. That will increase the value of the game by that constant, and
will have no effect on the equilibrium mixed strategies for the
equilibrium.
The equilibrium mixed strategy for the minimizing player can be found
by solving the dual of the given linear program. Or, it can be found by
using the above procedure to solve a modified payoff matrix which is
the transpose and negation of
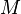
(adding a constant so it's positive), then solving the resulting game.
If all the solutions to the linear program are found, they will
constitute all the Nash equilibria for the game. Conversely, any linear
program can be converted into a two-player, zero-sum game by using a
change of variables that puts it in the form of the above equations. So
such games are equivalent to linear programs, in general.
[citation needed]
Non-zero-sum
Economics
Many economic situations are not zero-sum, since valuable goods and
services can be created, destroyed, or badly allocated in a number of
ways, and any of these will create a net gain or loss of utility to
numerous stakeholders. Specifically, all trade is by definition positive
sum, because when two parties agree to an exchange each party must
consider the goods it is receiving to be more valuable than the goods it
is delivering. In fact, all economic exchanges must benefit both
parties to the point that each party can overcome its
transaction costs, (or the transaction would simply not take place).
There is some semantic confusion in addressing exchanges under
coercion.
If we assume that "Trade X", in which Adam trades Good A to Brian for
Good B, does not benefit Adam sufficiently, Adam will ignore Trade X
(and trade his Good A for something else in a different positive-sum
transaction, or keep it). However, if Brian uses force to ensure that
Adam will exchange Good A for Good B, then this says nothing about the
original Trade X. Trade X was not, and still is not, positive-sum (in
fact, this non-occurring transaction may be zero-sum, if Brian's net
gain of utility coincidentally offsets Adam's net loss of utility). What
has in fact happened is that a new trade has been proposed, "Trade Y",
where Adam exchanges Good A for two things: Good B and escaping the
punishment imposed by Brian for refusing the trade. Trade Y is
positive-sum, because if Adam wanted to refuse the trade, he
theoretically has that option (although it is likely now a much worse
option), but he has determined that his position is better served in at
least temporarily putting up with the coercion. Under coercion, the
coerced party is still doing the best they can under their unfortunate
circumstances, and any exchanges they make are positive-sum.
There is additional confusion under
asymmetric information. Although many economic theories assume
perfect information,
economic participants with imperfect or even no information can always
avoid making trades that they feel are not in their best interest.
Considering transaction costs, then, no zero-sum exchange would ever
take place, (although asymmetric information can reduce the number of
positive-sum exchanges, as occurs in
The Market for Lemons).
See also:
Psychology
The most common or simple example from the subfield of
Social Psychology is the concept of "
Social Traps".
In some cases we can enhance our collective well-being by pursuing our
personal interests — or parties can pursue mutually destructive behavior
as they choose their own ends.
Complexity
It has been theorized by
Robert Wright in his book
Nonzero: The Logic of Human Destiny, that society becomes increasingly non-zero-sum as it becomes more complex, specialized, and interdependent. As former
US President Bill Clinton states:
The more complex societies get and the more complex
the networks of interdependence within and beyond community and
national borders get, the more people are forced in their own interests
to find non-zero-sum solutions. That is, win–win solutions instead of
win–lose solutions.... Because we find as our interdependence increases
that, on the whole, we do better when other people do better as well —
so we have to find ways that we can all win, we have to accommodate each
other....
—Bill Clinton,
Wired interview, December 2000.
[3]
Extensions
In 1944
John von Neumann and
Oskar Morgenstern proved that any zero-sum game involving
n players is in fact a generalized form of a zero-sum game for two players, and that any non-zero-sum game for
n players can be reduced to a zero-sum game for
n + 1 players; the (
n + 1) player representing the global profit or loss.
[4]
Misunderstandings
Zero–sum games and particularly their solutions are commonly
misunderstood by critics of game theory, usually with respect to the
independence and
rationality
of the players, as well as to the interpretation of utility functions.
Furthermore, the word "game" does not imply the model is valid only for
recreational
games.
[1]
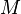 where element
where element  is the payoff obtained when the minimizing player chooses pure strategy
is the payoff obtained when the minimizing player chooses pure strategy 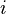 and the maximizing player chooses pure strategy
and the maximizing player chooses pure strategy 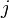 (i.e. the player trying to minimize the payoff chooses the row and the
player trying to maximize the payoff chooses the column). Assume every
element of
(i.e. the player trying to minimize the payoff chooses the row and the
player trying to maximize the payoff chooses the column). Assume every
element of  :
:
 ≥ 1.
≥ 1.![\begin{array}{rl}
{\displaystyle \min_{x^1, \ldots, x^n \in \mathbb{R}^n}} & {\displaystyle \sum_{i,j \in [n]} c_{i,j} (x^i \cdot x^j)} \\
\text{subject to} & {\displaystyle \sum_{i,j \in [n]} a_{i,j,k} (x^i \cdot x^j) \leq b_k \qquad \forall k}. \\
\end{array}](http://upload.wikimedia.org/wikipedia/en/math/f/8/8/f88255c018dce0154f44961e90618d9b.png)
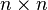 matrix
matrix  such that
such that  for all
for all  ). If this is the case, we denote this as
). If this is the case, we denote this as  . Note that there are several other equivalent definitions of being positive semidefinite.
. Note that there are several other equivalent definitions of being positive semidefinite. the space of all real symmetric matrices. The space is equipped with the
the space of all real symmetric matrices. The space is equipped with the  denotes the
denotes the 

 is given by
is given by  from the previous section and
from the previous section and  is an
is an  from the previous section.
from the previous section.
 as a diagonal entry (
as a diagonal entry ( for some
for some  , constraints
, constraints  can be added for all
can be added for all  . As another example, note that for any positive semidefinite matrix
. As another example, note that for any positive semidefinite matrix 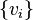 such that the
such that the  the
the 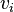 and
and  .
Therefore, SDPs are often formulated in terms of linear expressions on
scalar products of vectors. Given the solution to the SDP in the
standard form, the vectors
.
Therefore, SDPs are often formulated in terms of linear expressions on
scalar products of vectors. Given the solution to the SDP in the
standard form, the vectors 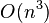 time (e.g., by using an incomplete
time (e.g., by using an incomplete 

 and
and  ,
,  means
means  .
.
 such that
such that  ,
,  ). Then there is an optimal solution
). Then there is an optimal solution  to (D-SDP) and
to (D-SDP) and
 for some
for some  ). Then there is an optimal solution
). Then there is an optimal solution  to (P-SDP) and the equality from (i) holds.
to (P-SDP) and the equality from (i) holds. ,
, 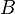 , and
, and 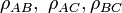 are valid if and only if
are valid if and only if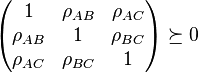
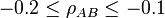 and
and  . The problem of determining the smallest and largest values that
. The problem of determining the smallest and largest values that  can take is given by:
can take is given by:



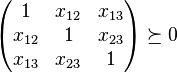
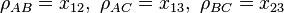 to obtain the answer. This can be formulated by an SDP. We handle the
inequality constraints by augmenting the variable matrix and introducing
to obtain the answer. This can be formulated by an SDP. We handle the
inequality constraints by augmenting the variable matrix and introducing

 as
as  and
and  respectively.
respectively.
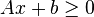
 whenever
whenever  the problem can be reformulated:
the problem can be reformulated:
 .
.
 is the square matrix with values in the diagonal equal to the elements of the vector
is the square matrix with values in the diagonal equal to the elements of the vector  .
.
![\underbrace{\left[\begin{array}{cc}t&c^Tx\\c^Tx&d^Tx\end{array}\right]}_{D}\geq 0](http://upload.wikimedia.org/wikipedia/en/math/4/7/1/4716c3a1c00adcf62801a21e76330fdb.png)
 .
.![\left[\begin{array}{ccc}\textbf{diag}(Ax+b)&0&0\\0&t&c^Tx\\0&c^Tx&d^Tx\end{array}\right] \succeq 0](http://upload.wikimedia.org/wikipedia/en/math/a/7/3/a73fe310dadd0470b5e627217fa60e1a.png)
 such that each
such that each  .
. ).
). such that
such that  , where the maximization is over vectors
, where the maximization is over vectors 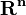 ;
since the vectors are not required to be collinear, the value of this
relaxed program can only be higher than the value of the original
quadratic integer program. Finally, a rounding procedure is needed to
obtain a partition. Goemans and Williamson simply choose a uniformly
random hyperplane through the origin and divide the vertices according
to which side of the hyperplane the corresponding vectors lie.
Straightforward analysis shows that this procedure achieves an expected approximation ratio
(performance guarantee) of 0.87856 - ε. (The expected value of the cut
is the sum over edges of the probability that the edge is cut, which is
proportional to the angle
;
since the vectors are not required to be collinear, the value of this
relaxed program can only be higher than the value of the original
quadratic integer program. Finally, a rounding procedure is needed to
obtain a partition. Goemans and Williamson simply choose a uniformly
random hyperplane through the origin and divide the vertices according
to which side of the hyperplane the corresponding vectors lie.
Straightforward analysis shows that this procedure achieves an expected approximation ratio
(performance guarantee) of 0.87856 - ε. (The expected value of the cut
is the sum over edges of the probability that the edge is cut, which is
proportional to the angle  between the vectors at the endpoints of the edge over
between the vectors at the endpoints of the edge over  . Comparing this probability to
. Comparing this probability to  , in expectation the ratio is always at least 0.87856.) Assuming the
, in expectation the ratio is always at least 0.87856.) Assuming the  .
.