Stochastic matrix
From Wikipedia, the free encyclopedia
- For a matrix whose elements are stochastic, see Random matrix
- A right stochastic matrix is a square matrix each of whose rows consists of nonnegative real numbers, with each row summing to 1.
- A left stochastic matrix is a square matrix each of whose columns consist of nonnegative real numbers, with each column summing to 1.
- A doubly stochastic matrix is a square matrix where all entries are nonnegative and all rows and all columns sum to 1.
A common convention in English language mathematics literature is to use row vectors of probabilities and right stochastic matrices rather than column vectors of probabilities and left stochastic matrices; this article follows that convention.
Contents |
Definition and properties
A stochastic matrix describes a Markov chain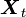 over a finite state space S.
over a finite state space S.If the probability of moving from
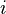 to
to 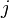 in one time step is
in one time step is 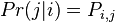 , the stochastic matrix P is given by using
, the stochastic matrix P is given by using 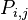 as the
as the  row and
row and  column element, e.g.,
column element, e.g.,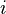 to some state must be 1, this matrix is a right stochastic matrix, so that
to some state must be 1, this matrix is a right stochastic matrix, so that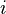 to
to 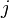 in two steps is then given by the
in two steps is then given by the 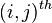 element of the square of
element of the square of 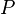 :
: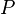 in k steps is given by
in k steps is given by  .
.An initial distribution is given as a row vector.
A stationary probability vector
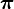 is defined as a vector that does not change under application of the transition matrix; that is, it is defined as a left eigenvector of the probability matrix, associated with eigenvalue 1:
is defined as a vector that does not change under application of the transition matrix; that is, it is defined as a left eigenvector of the probability matrix, associated with eigenvalue 1: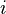 we have the following limit,
we have the following limit, is the
is the  element of the row vector
element of the row vector 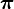 . This implies that the long-term probability of being in a state
. This implies that the long-term probability of being in a state 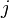 is independent of the initial state
is independent of the initial state 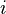 . That either of these two computations give one and the same stationary vector is a form of an ergodic theorem, which is generally true in a wide variety of dissipative dynamical systems: the system evolves, over time, to a stationary state.
Intuitively, a stochastic matrix represents a Markov chain with no sink
states, this implies that the application of the stochastic matrix to a
probability distribution would redistribute the probability mass of the
original distribution while preserving its total mass. If this process
is applied repeatedly the distribution converges to a stationary
distribution for the Markov chain.
. That either of these two computations give one and the same stationary vector is a form of an ergodic theorem, which is generally true in a wide variety of dissipative dynamical systems: the system evolves, over time, to a stationary state.
Intuitively, a stochastic matrix represents a Markov chain with no sink
states, this implies that the application of the stochastic matrix to a
probability distribution would redistribute the probability mass of the
original distribution while preserving its total mass. If this process
is applied repeatedly the distribution converges to a stationary
distribution for the Markov chain.Example: the cat and mouse
Suppose you have a timer and a row of five adjacent boxes, with a cat in the first box and a mouse in the fifth box at time zero. The cat and the mouse both jump to a random adjacent box when the timer advances. E.g. if the cat is in the second box and the mouse in the fourth one, the probability is one fourth that the cat will be in the first box and the mouse in the fifth after the timer advances. If the cat is in the first box and the mouse in the fifth one, the probability is one that the cat will be in box two and the mouse will be in box four after the timer advances. The cat eats the mouse if both end up in the same box, at which time the game ends. The random variable K gives the number of time steps the mouse stays in the game.The Markov chain that represents this game contains the following five states:
- State 1: cat in the first box, mouse in the third box: (1, 3)
- State 2: cat in the first box, mouse in the fifth box: (1, 5)
- State 3: cat in the second box, mouse in the fourth box: (2, 4)
- State 4: cat in the third box, mouse in the fifth box: (3, 5)
- State 5: the cat ate the mouse and the game ended: F.
Long-term averages
As state 5 is an absorbing state the long-term average vector . Regardless of the initial conditions the cat will eventually catch the mouse.
. Regardless of the initial conditions the cat will eventually catch the mouse.Phase-type representation
As the game has an absorbing state 5 the distribution of time to absorption is discrete phase-type distributed. Suppose the system starts in state 2, represented by the vector![[0,1,0,0,0]](http://upload.wikimedia.org/wikipedia/en/math/c/e/f/cef4c5c8b47551c16f5cf1829f455852.png) . To simplify the calculations, state five can be ignored. Let
. To simplify the calculations, state five can be ignored. Let with
with 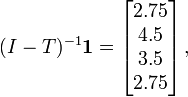
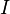 is the identity matrix, and
is the identity matrix, and 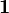 represents a column matrix of all ones. The expected time of the mouse's survival is given by
represents a column matrix of all ones. The expected time of the mouse's survival is given bySee also
- Muirhead's inequality
- Perron–Frobenius theorem
- Doubly stochastic matrix
- Discrete phase-type distribution
- Probabilistic automaton
- Models of DNA evolution
References
- G. Latouche, V. Ramaswami. Introduction to Matrix Analytic Methods in Stochastic Modeling, 1st edition. Chapter 2: PH Distributions; ASA SIAM, 1999.

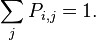





![\boldsymbol{\tau}=[0,1,0,0]](http://upload.wikimedia.org/wikipedia/en/math/4/5/6/4561947495736c2c9ade968c97ff25b8.png)
![E[K]=\boldsymbol{\tau}(I-T)^{-1}\boldsymbol{1}=4.5.](http://upload.wikimedia.org/wikipedia/en/math/b/6/4/b642b25d3bc3cc4e29b8a0db0d621dd1.png)
![E[K(K-1)\dots(K-n+1)]=n!\boldsymbol{\tau}(I-{T})^{-n}{T}^{n-1}\mathbf{1}\,.](http://upload.wikimedia.org/wikipedia/en/math/5/7/c/57c5350719a812734acc73301de274bc.png)
No comments:
Post a Comment
Thank you